This week’s question comes from T.W., who asks:
Does anyone track errors against for a hitter? It would seem to me that this
might be a consistent skill (due to speed, an ability to consistently hit
hard ground balls, and continued hustle). If it is a consistent skill
shouldn’t this be tracked and shouldn’t certain players get recognition for
this? I would think that historically Pete Rose would have
"caused" more errors than someone like Ken Griffey Jr. due
simply to hitting style and hustle. So, my question is, can this be
measured? If so, who are the great players historically and today? If so,
shouldn’t this be accounted for in a players OBP?
Thanks, T.W. This is one of the most common questions I’ve gotten over the
years between BP.com and my own Stathead.com
Web sites. Fortunately, with the availability of play-by-play data over the past
couple of decades, it’s possible to investigate this properly.
I have play-by-play data for 1978-2000, so all of the analysis in this
article will cover just those years. My first step was to look at the yearly
totals, to see what the highest seasonal totals for reached-on-error (ROE)
have been. Only four players have reached base via error 20 or more times in
a single season, but some of them probably aren’t who you’d expect:
Year Player ROE 1979 Jack Clark 21 1986 Willie McGee 21 1998 Derek Jeter 20 1986 Carney Lansford 20 1984 Steve Sax 17 1982 Rafael Ramirez 17 1979 Al Cowens 17 1991 Cal Ripken Jr. 17 1985 Tommy Herr 16 1982 Pedro Guerrero 16 1993 Darren Lewis 16 1989 Roberto Alomar 16 1998 Vinny Castilla 16 1978 Larry Bowa 16 1984 Ryne Sandberg 16 1996 Marquis Grissom 16 1983 Ryne Sandberg 15 1983 Tim Wallach 15 1984 Julio Franco 15 1984 Brett Butler 15 1982 Paul Molitor 15 1990 Joe Carter 15 1990 Shawon Dunston 15
Willie McGee you might have guessed, as he fits the speedy profile
you naturally suspect of having an ROE ability. But Jack Clark? Not
only is he not thought of as particularly swift afoot (though he did have 11
steals in 1979), but he’s also one of the Three True Outcome demigods, with
over 37% of his career PA ending without him putting the ball in play. And
while there’s more speedsters on the list, there are some surprising names
like Clark, Tim Wallach, and Vinny Castilla, too.
Of course, we’re looking at raw totals, and not rates. Getting a lot of
plate appearances will help you rack up the ROE totals, regardless of
ability. So next we’ll look at the highest ROE% (percentage of plate
appearances ending with the batter reaching base on error):
Limiting the set of players to those with 500 or more plate appearances, the
list of seasons with a ROE% or 2.5% or greater is:
Player ROE PA ROE% Willie McGee 21 539 3.90% Jack Clark 21 598 3.51% Carney Lansford 20 640 3.13% Al Cowens 17 568 2.99% Derek Jeter 20 694 2.88% Darren Lewis 16 572 2.80% Steve Sax 17 622 2.73% Shawon Dunston 15 573 2.62% Rafael Ramirez 17 669 2.54%
All of the players on this list are also represented on the previous list.
Only 86 out of the 1704 player-seasons represented topped 2% ROE, so we are
talking about a fairly small impact on OBP if we were to include it,
probably comparable to or slightly less significant than hit-by-pitches.
The next step is to ask whether the tendency to reach base on error persists
from year to year (thus indicating some level of ability innate to the
player). I’ve plotted ROE rates in consecutive seasons for players with 500+
plate appearances in both seasons in the chart below:
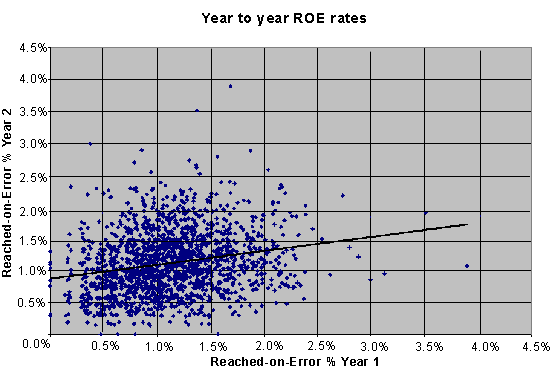
The correlation between year 1 ROE% and year 2 ROE% is 0.2183, which means
there’s a slight relationship there, but not terribly strong (less than 5%
of the year-to-year variance can be explained by differences in ability
among players). Of course, we’re talking about an event with pretty low
frequency anyway, so it’s easy for a true effect to get lost in the small
sample sizes of a single season.
What if we borrow
a technique I used in analyzing Voros McCracken’s DIPS
research, and split each player’s career into even- and odd-numbered halves
(1000+ PA in each half) and see if the evidence for ROE ability is any
stronger?
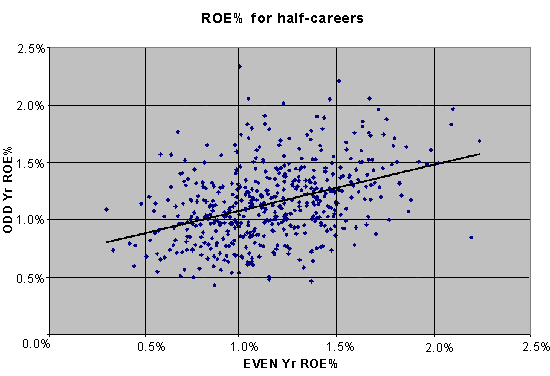
It may not be clear at first glance, but there is actually a significantly
more distinct linear trend in the chart above versus the year-to-year chart
presented earlier. The correlation between the ROE% in the even-year
half-career and the odd-year half-career jumps to 0.4114, with more than 16%
of the variance now attributable to ability.
So there’s decent evidence that reaching base via error is at least
partially due to the ability of the batter, ranging from about 0.75% to
1.75% or so for most players. It’s difficult to spot using just a single
year’s worth of data, but using career ROE% to date is not a bad way to set
an expectation for the future.
As for its effect on OBP, there’s a reasonable argument to be made to
include it, as it does partially reflect the skill of the batter to avoid an
out by inducing an error. However, since all players would get somewhat of a
boost from including it, the importance of the effect is how much we might
overrate or underrate a player’s OBP relative to his peers by not including
ROE%.
As it turns out, the effect is rather small. The standard deviation in
career ROE% for our half-career subset (about 500 players) is 2.7 points of
OBP, meaning that more than 90% of players would be within five points of
the OBP they would have as currently measured plus the league-average boost
in ROE%. So while it makes some logical sense to include ROE% in OBP, we’re
probably not missing a huge piece of the sabermetric puzzle by not having it
in the standard calculation.
However, we can’t let a topic like this go by without at least sharing the
career leaders. So we’ll close with a couple of tables, one of the players
with the highest career ROE%, and the other of the lowest career ROE%.
Highest career ROE% (min: 2000 PA), 1978-2000
Player ROE PA ROE% Bob Horner 86 4213 2.041% Rudy Law 53 2647 2.002% Johnny Bench 47 2365 1.987% Wil Cordero 71 3635 1.953% Billy Sample 52 2798 1.858% Garry Maddox 63 3431 1.836% Glenn Hubbard 94 5122 1.835% John Castino 47 2578 1.823% Rey Sanchez 64 3557 1.799% Derek Jeter 64 3565 1.795% Ricky Jordan 39 2221 1.756% Rafael Ramirez 103 5887 1.750% Willie McGee 143 8188 1.746% Milt May 37 2124 1.742% Otis Nixon 101 5800 1.741% Bob Dernier 48 2757 1.741% Mark Carreon 38 2190 1.735% Johnnie LeMaster 55 3179 1.730% Al Wiggins 44 2553 1.723% Jose Vizcaino 73 4244 1.720% Luis Salazar 75 4375 1.714% Ron Jackson 42 2466 1.703%
Lowest career ROE% (min: 2000 PA), 1978-2000
Player ROE PA ROE% John Mayberry 9 2351 0.383% Mo Vaughn 26 5756 0.452% Willie Greene 10 2183 0.458% Ken Phelps 11 2287 0.481% Paul Sorrento 20 3890 0.514% Chad Kreuter 14 2569 0.545% Darren Daulton 24 4340 0.553% Jeromy Burnitz 19 3254 0.584% Luis Alicea 23 3923 0.586% Darrin Fletcher 22 3683 0.597% Rico Brogna 18 3000 0.600% Geno Petralli 13 2131 0.610% Carlos Delgado 21 3430 0.612% Rafael Palmeiro 55 8942 0.615% Pat Kelly 14 2237 0.626% Ray Lankford 36 5741 0.627% Rusty Staub 14 2213 0.633% Jim Dwyer 17 2673 0.636% Darin Erstad 18 2811 0.640% Carl Yastrzemski 19 2963 0.641% Ernie Whitt 27 4206 0.642% Matt Stairs 16 2487 0.643%
Keith Woolner is an author of Baseball Prospectus. You can contact him by
clicking here.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now