Do the Data Support the Commissioner’s Report on the Astros’ Sign-Stealing Scandal?

In January, Baseball Prospectus’ Robert Arthur analyzed the effectiveness of the 2017 Houston Astros’ sign-stealing scheme. To do so, he used a dataset created by disheartened Astros fan Tony Adams, who charted every pitch of almost every 2017 Astros home game. Adams identified the batter, opponent, pitch type, pitch outcome, runners on base, and most critically, whether or not there was an audible bang before each pitch. Banging was intrinsic to the Astros’ scheme, as they would bang if and only if the impending pitch were offspeed.

This dataset is particularly helpful because it reveals for every pitch whether the sign-stealing was accurate. Specifically, accurate refers to a bang before an offspeed pitch or no bang before a fastball. On the other hand, inaccurate refers to a bang before a fastball or no bang before an offspeed pitch. Arthur found that the Astros did not always accurately steal signs. Furthermore, the cost of the inaccuracies ultimately canceled out any benefits the scheme provided.

Inspired in part by Arthur’s research, we conducted our own study on Adams’s dataset. First, we addressed Arthur’s question: How effective was the Astros’ scheme? Like him, but with different specifications, we found that because the Astros did not always correctly decode the opposing signs, their scheme was not particularly effective. Also, we addressed a second question: Are there any telltale patterns of cheating that can indicate whether the cheating stopped in 2018 or continued through 2019? While the data cannot tell us whether the Astros cheated in 2019, we did find a particularly interesting pattern. What follows is a condensed edition of our study.

Part 1: Houston Astros 2017 Banging Scheme

First, we run logistic regressions on Adams’s dataset to find whether sign-stealing benefitted the Astros on a pitch-by-pitch basis. Logistic regressions are used when the dependent variables are binary dummy variables, that is, equal to 1 or 0. Our first dependent variable is SWING, which equals 1 if the batter swings at a pitch. Our second is CALL STR, which applies to taken pitches. It equals 1 if the umpire calls a taken pitch a strike. In contrast, our last four dependent variables apply to swings, not takes. These variables partition swings into four outcomes: whiffs (WHIFF), foul balls (FOUL), balls in play (IN PLAY), and home runs (HR). We do not break IN PLAY down further into hits versus outs because the effects of cheating on hits versus outs are nearly identical.

Meanwhile, our independent variables, which are also dummies, are CHEATING, ACCURATE, and INACCURATE. Specifically, CHEATING equals 1 if a pitch comes from a plate appearance with at least one bang. In contrast, if a pitch comes from a plate appearance with no bangs, the Astros most likely were not cheating in that plate appearance. However, we have to be careful because the trash can operator did not bang for impending fastballs. Therefore, we drop all pitches from plate appearances that lack an offspeed pitch. We also drop all pitches from plate appearances with a runner on second base. The reason is that with a runner on second, the Astros sometimes abandoned the trash can in favor of letting the runner signal to the batter.

While CHEATING applies to all pitches in our sample, ACCURATE and INACCURATE only apply to pitches where CHEATING equals 1. Specifically, ACCURATE equals 1 when the pitch is a fastball with no bangs or an offspeed pitch with a bang. On the other hand, INACCURATE equals 1 when it is a fastball with a bang or an offspeed pitch with no bangs. We find that when the Astros cheated, they correctly identified the incoming pitch 82.0 percent of the time.

In Table 1, we regress each dependent variable, first on CHEATING and then on ACCURATE and INACCURATE. In addition, each regression has batter-opponent fixed effects. An example of a fixed effect is Jose Altuve batting against the Oakland Athletics. These effects control for differences between some batters, such as Altuve, who used the scheme less often than other batters, such as Marwin Gonzalez. In addition, losing teams often did not try as hard as winning teams to protect their signs. As a result, omitting the effects could bias our coefficient estimates.

Table 1: Logistic Regressions with 215 Batter-Opponent Fixed Effects, Tony Adams’s Dataset
Cheating vs. Not Cheating	Variable	(1) SWING	(2) CALL STR	(3) WHIFF	(4) FOUL	(5) IN PLAY	(6) HR
	CHEATING	0.061	0.071	-0.245	0.370	-0.106	-1.157
		(p = 0.479)	(p = 0.572)	(p = 0.112)	(p = 0.005)	(p = 0.445)	(p = 0.022)
	Includes	Pitches	Takes	Swings	Swings	Swings	Swings
	Observations	5,183	2,866	2,086	2,231	2,189	676
	Pseudo R2	0.000	0.000	0.001	0.003	0.000	0.026
Accurate vs. Inaccurate vs. Not Cheating	Variable	(7) SWING	(8) CALL STR	(9) WHIFF	(10) FOUL	(11) IN PLAY	(12) HR
	ACCURATE	0.125	0.001	-0.486	0.495	-0.039	-1.147
		(p = 0.171)	(p = 0.996)	(p = 0.004)	(p < 0.001)	(p = 0.793)	(p = 0.030)
	INACCURATE	-0.133	0.276	0.449	-0.014	-0.328	-1.196
		(p = 0.288)	(p = 0.114)	(p = 0.038)	(p = 0.945)	(p = 0.133)	(p = 0.139)
	ACC vs. INACC	p = 0.033	p = 0.094	p < 0.001	p = 0.010	p = 0.182	p = 0.951
	Includes	Pitches	Takes	Swings	Swings	Swings	Swings
	Observations	5,183	2,866	2,086	2,231	2,189	676
	Pseudo R2	0.001	0.001	0.012	0.006	0.001	0.026

Per the top half of Table 1, CHEATING’s largest effects were on WHIFF, FOUL, and HR. Specifically, CHEATING decreased the rate of whiffs per swings, increased the rate of fouls per swings, and decreased the rate of home runs per swings. Therefore, the data support Arthur’s conclusion that cheating did not help the Astros much. While it helped them avoid whiffs, those would-be whiffs got turned into fouls rather than balls in play. Moreover, it hurt their power.

Furthermore, one of the reasons cheating was relatively ineffective is that the Astros’ 82.0 percent accuracy rate was not high enough. In the bottom half of Table 1, we show that the Astros hit better when cheating accurately than when cheating inaccurately. When cheating accurately, their whiff rate decreased, and their foul rate increased relative to when they did not cheat. However, when cheating inaccurately, their called strike rate increased, whiff rate increased, in-play rate decreased, and home run rate decreased relative to when they did not cheat.

Interestingly, their home run rate decreased when cheating whether they cheated accurately or not. It seems like Astros batters changed their swing style when cheating in a way that favored contact over power. Such a change could have easily been unintentional and resulted from a lack of experience in hitting while stealing signs. Finally, we see that the Astros swung more often when cheating accurately than when cheating inaccurately. It is unclear whether swinging more often is good or bad, but this information proves useful for examining data outside Adams’s dataset. Overall, like Arthur, we conclude that cheating did not help the Astros much on the whole, but they hit better when cheating accurately than inaccurately.

Part 2: Potential Evidence of Further Sign-Stealing

In this part, we look for sign-stealing in all Astros games from 2017 through 2019 rather than just in 2017 home games. Unfortunately, we can no longer know which pitches the Astros were cheating on. However, we can take the patterns from Adams’s dataset and apply them to Statcast pitch-by-pitch data from 2008 to 2019. Because of reports that cheating may have occurred on the road as well as at home, we include road games in our sample. Also, while we began from the belief that cheating occurred in 2017 and 2018, we are initially agnostic in regard to 2019.

We know from Adams’s dataset that the Astros’ performance differed when cheating accurately than inaccurately. Therefore, to identify cheating outside that dataset, we need a proxy variable correlated with accuracy. One such variable is whether a runner is on second base. Adams’s dataset cannot tell us if cheating is more or less accurate with a runner on second since the Astros sometimes used silent methods with a runner on second. But because catchers often use more complex signs with a runner on second, cheating should be less accurate and occur less often.

As such, we analyze six dependent variables: swing rate split, called strike rate split, whiff rate split, foul rate split, in-play rate split, and home run rate split. Each split is defined as the rate in question without a runner on second (when the cheating should be more accurate and prevalent) minus that rate with a runner on second (when the cheating should be less accurate and prevalent). Then, in Figure 1, we provide line graphs illustrating how the Astros’ splits changed over time relative to those of other teams. For each graph, the y axis is the split for the given rate, the x axis is the year, the red line charts the highest split in each year, the blue line charts the lowest split in each year, the orange line charts the Astros’ split in each year, and the black line charts the composite of other teams’ splits in each year. In our full study, we corroborate our line graphs with a statistical technique called difference in differences regressions.

We start with the following expectations. First, the Astros should have a relatively high swing rate split in 2017 and 2018. The reason is that the Astros’ swing rate was highest when cheating accurately. Second, they should have a relatively low called strike rate split in 17-18 because their called strike rate was highest when cheating inaccurately, but cheating accurately had almost the same effect as not cheating. Third, they should have a relatively low whiff rate split in 17-18 because their whiff rate was lowest when cheating accurately. Finally, they should have a relatively high foul rate split in 17-18 because their foul rate was highest when cheating accurately. In contrast, their expected in-play and home run rate splits are ambiguous because their in-play and home run rates were lowest when cheating inaccurately but highest when not cheating. Recall that with a runner on second, cheating is less likely to be accurate and to occur.

Figure 1: Difference in Differences Graphs of 2B Splits, Statcast Dataset 2008-2019

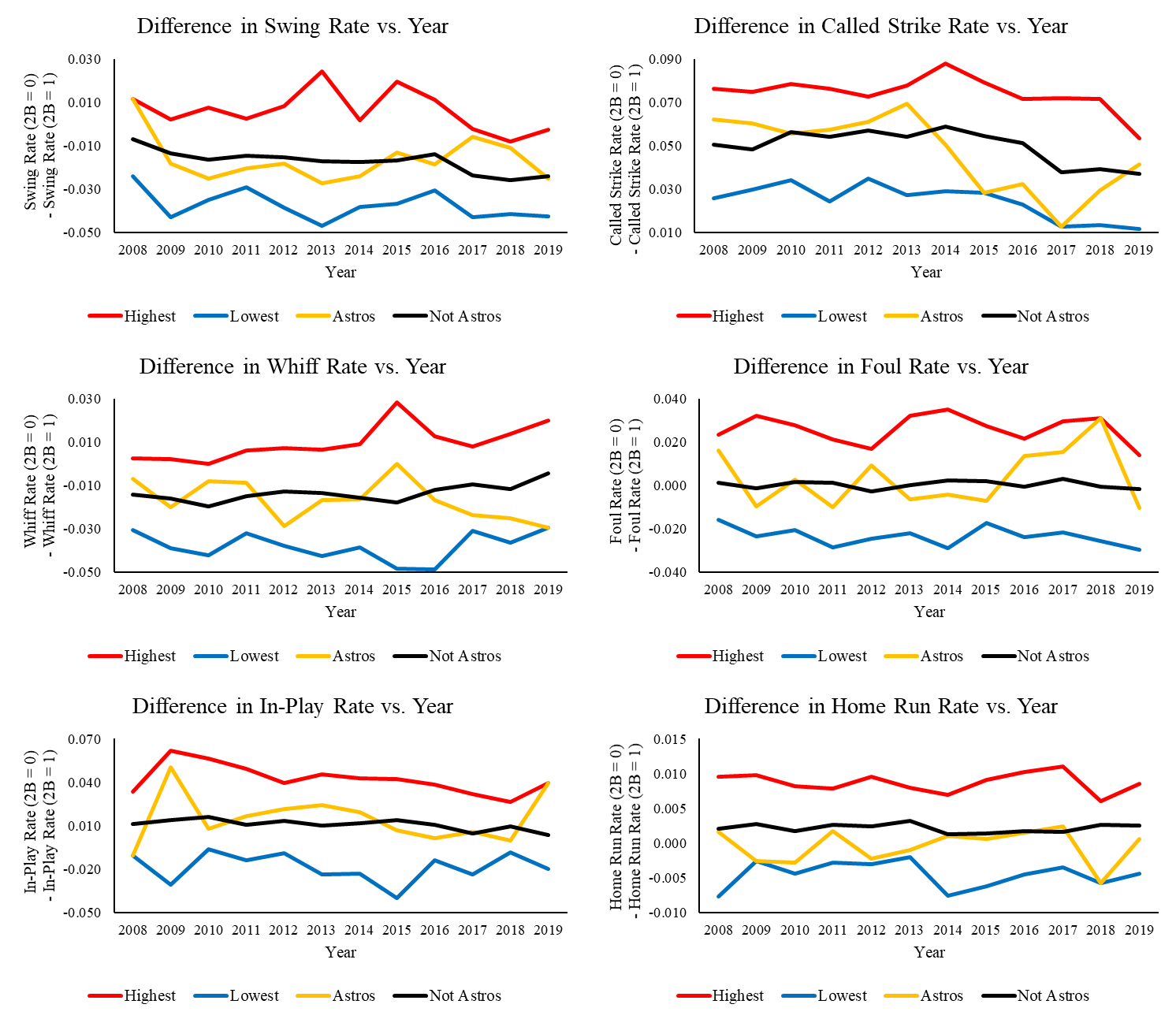
As shown in Figure 1, the results meet our expectations. The Astros’ swing rate split was relatively high in 2017 and 2018, their called strike rate split was relatively low, their whiff rate split was relatively low, and their foul rate split was relatively high. Therefore, like Manfred, we conclude that the Astros cheated in 2017 and 2018. But what about 2019? In 2019, the Astros’ swing, called strike, and foul rate splits reverted back to normal. But their whiff rate split was the lowest in baseball, and their in-play rate split surged to the highest in baseball. In addition, we can combine balls in play that are not home runs with home runs, and we can call this split the fair ball split. It turns out that the 2019 Astros also had the highest fair ball split in baseball. 

Therefore, there are three possibilities. The first possibility is that Manfred correctly concluded that the Astros did not cheat in 2019, and their unusual whiff, in-play, and fair ball rate splits are statistical flukes. In contrast, the second possibility is that the Astros got better at cheating in 2019. Specifically, there are two ways to get better at cheating. The first way is to cheat only when confident the stolen signs are accurate. If the Astros made this improvement, they would have cheated less often with a runner on second. Thus, their swing and called strike rates would revert to normal because there would be fewer cases of inaccurate cheating. In fact, per Adams’s dataset, there is virtually no difference between called strike rates when cheating accurately and those when not cheating. Furthermore, the second way is to learn to put balls into play when cheating accurately (rather than foul them off). Doing so would lead to the observed decrease in the Astros’ foul rate split, along with the observed increases in their in-play and home run rate splits. Meanwhile, their whiff rate split would remain low, as we also observed. As such, there is evidence to support the belief among many players that despite additional anti-sign stealing rules implemented before the 2019 season, the Astros continued cheating in 2019.

However, the third possibility is that the Astros did not cheat in 2019, but their unusual splits are not statistical flukes. Rather, because other teams believed the Astros were cheating with nobody on second, those teams may have been thrown off their game. In the words of AJ Hinch during the 2019 ALCS against the New York Yankees, who suspected the Astros of whistling to convey stolen signs, “Had I known that it would take something like [whistling noises] to set off the Yankees or any other team, we would have practiced it in Spring Training. It apparently works, even when it doesn’t happen.” All in all, while the data cannot tell us whether the Astros cheated in 2019, the data can provide valuable insight into what may have happened last season.