Best of BP: We’re Talking About Seam-Shifted Wake Wrong

Every year, it seems that there’s a new metric that further explains the intricacies of the game of baseball. A decade ago, that was batting average on balls in play, which helped us to understand the variability of outcomes on balls in play. A few years ago, there was launch angle, which was oft-cited as the rationale behind the so-called fly ball revolution. Now? Seam-shifted wake (SSW) has usurped spin rate as the hot topic of the past year or so, but it seems that the public is lagging behind in terms of our understanding of it.

The term SSW, coined by Andrew Smith, attempts to explain non-Magnus and drag movement caused by the seams on the baseball or, in other words, movement that isn’t caused by the spin of the baseball. Pitches with a heavy SSW component create turbulence on one side of the baseball, creating force that is asymmetrical and causes unexpected movement, often referred to by fans and scouts alike as late movement. SSW is a way of creating movement that more commonly comes from different arm slots than the respective pitcher. To hitters, the movement is incongruent from how they expect the ball to move based on its spin at release. In other words, SSW can be a form of deception.

Before we zoom out and look at SSW at the macro level, it makes sense to show common examples of SSW, and what people often look for to know what actually constitutes a pitch with SSW.

First, one of my favorite pitches in baseball, Paul Sewald’s slider:

As far as hitters go, Andrew Vaughn is a good one, and he doesn’t chase pitches out of the zone more than your average hitter, so it makes you raise your eyebrows when he chases a pitch that’s so far out of the zone. Why’d he chase here? Because Sewald is impossible. He’s equipped with one of the best fastballs in MLB and a frisbee slider with huge sweep that moves much differently than you’d expect based on his pitch characteristics at release.

To begin in illustrating why that’s the case, here’s a graphic showing Sewald’s spin direction at release, versus when it arrives at the plate:

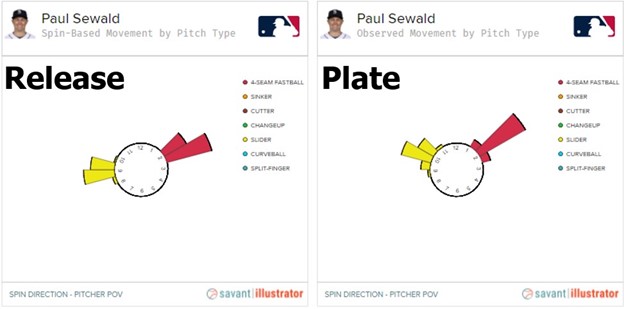
Compared to his spin direction at release, Sewald’s slider has shifted upwards, on average, from 8:45 on a clock face to 9:15 according to Baseball Savant, or 8:28 to 9:54 according to Texas Leaguers. Its shifting upwards means that he gets more ride on his slider than expected, but more importantly, it gets more cutting action, too. The result is a slider that drops less than expected, but gets more sweep, both of which explain the frisbee-like movement of the pitch. That makes it awfully difficult for the batter to figure out where the ball is going to end up and get the barrel to the ball, let alone make hard contact.

Here are Sewald’s expected and actual movement numbers on his fastball and slider, which can illustrate and quantify how surprising and deceptive his movement can be:

	xIVB	IVB	xHB	HB
Fastball	12.6	13.6	11.9	12.5
Slider	0.2	5.8	8.0	13.4

Here, we have a more objective look at how different Sewald’s pitches are in comparison to their expected movement, which is modeled based on spin rate, active spin rate, and spin direction. His fastball gets an extra inch of added ride, and about a half-inch of extra arm-side movement – that’s part of what’s made it such a devastating pitch. Perhaps more relevant, though, is that his slider gets 5.6 inches of added ride and 5.4 inches of added sweep, which adds up to 11 inches of additional non-Magnus movement. In terms of non-Magnus sweep on sliders, Sewald ranks in the 97th percentile, which makes this an elite pitch in terms of SSW.

Of course, it seems intuitive, but it’s worth considering whether this discrepancy in expected and actual movement bears out positive results. Here, we consider the relationship between movement differential (actual versus expected movement) and run value per 100 pitches (RV/100), for sinkers:

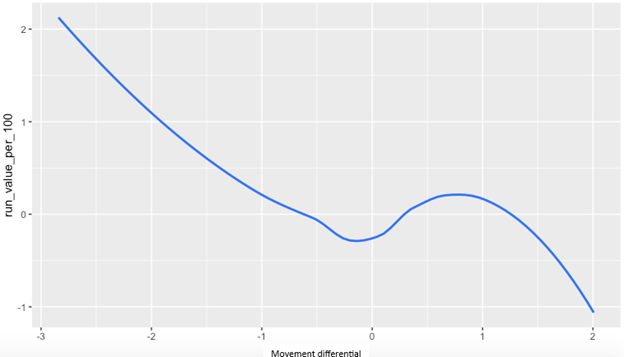
For the most part, there’s a negative relationship between movement differential and RV/100, which means that the larger the movement differential, the better the pitch performs. It’s pretty intuitive: the more the pitch moves differently than expected, the harder it is for hitters to make quality contact with the ball. Again, we’re talking about deception here. If we’re to accept this as a truth – and, based on the data, we should – then we ought to be able to substitute axis deviation in place of movement differential (our proxy for SSW) if the two are as interchangeable as they’re made out to be.

Again, we have RV/100 on the y-axis, but this time, axis deviation has replaced movement differential on the x-axis, again, for sinkers:

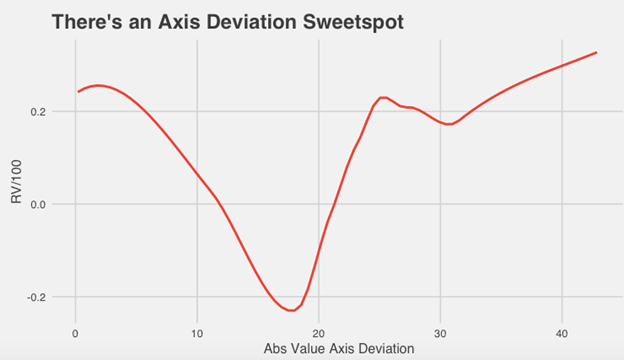
The graph descends just like the previous graph, and bottoms out around 17 and 18 degrees of axis deviation, but rises immediately, creating a positively skewed distribution. This means that, even though it’s been suggested that more axis deviation is good, the graph suggests otherwise. Too little axis deviation is likely to lead to poor results, but too much axis deviation is just as bad. And so, as with most things, there appears to be a sweet spot of axis deviation for sinkers.

It’s understandable why people would attempt to capture SSW by looking at axis deviation, because more gyro spin (or inactive spin) creates more axis deviation, and axis deviation is a necessary component of SSW. But, it’s not the only component. There’s a misunderstanding about the physics of baseball that’s created a disconnect about SSW on the public side, and a quick explanation should clarify the graph above.

To best illustrate this, it’s probably best to think on the extreme ends of active spin, or spin efficiency. On one end, you have a fastball or sinker with 100 percent spin efficiency, which means it has perfect backspin. On the other end, you have a gyro slider with zero percent spin efficiency, meaning it spins like a bullet.

Pure transverse spin vs. pure gyro spin

courtesy BaseballCloud’s BallR tool

The fastball gets a lot of added ride because 100 percent of its raw spin is converted into upward Magnus movement; the ball opposes gravity, which keeps it from falling as fast as it would otherwise. As for the gyro slider, the only downward movement that it gets is the result of gravity and the amount of horizontal movement is dependent on how much the ball is dropping and how much sidespin is added to the pitch on the way to the plate.

The fastball described above is much like a Gerrit Cole fastball, while the gyroball is more of a Shane Bieber slider. The fastball would rise, if not for the forces of gravity, while the gyroball wouldn’t move vertically at all – it just floats through space.

This is instructive in terms of our understanding of SSW. In general, the more active spin a pitch has, the more Magnus movement it gets. The less active spin, the less Magnus movement it gets. As shown above, there’s a sweet spot of axis deviation, so it seems pertinent to show a few examples of pitchers that throw pitches that move more than expected, less than expected, and as expected.

Here, Garrett Whitlock’s spin direction, at release and once his pitches arrive at the plate:

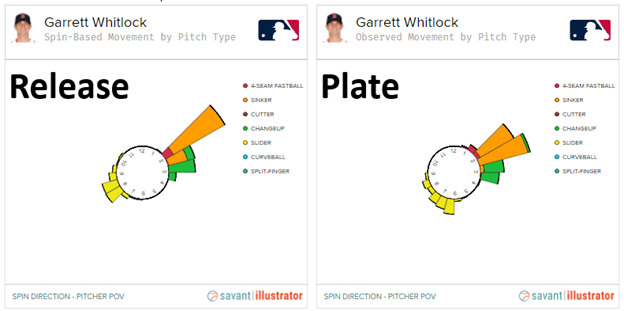
Just glancing at the chart it maybe looks like there’s a slight arm-side shift in Whitlock’s sinker tilt. The numbers reflect that, sort of, with Whitlock moving, on average, from a 1:30 tilt at release to 1:45 at the plate, but when you look more granularly, he’s actually moving from 1:37 to 1:49, which is one of the smallest axis deviations of all sinkers. That’s because, at 99.5 percent, Whitlock spins his sinker with almost pure spin efficiency. Because SSW requires a gyro component to take effect, his sinker moves almost exactly as expected given his pitch characteristics at release or, put another way, his sinker movement is essentially all Magnus movement.

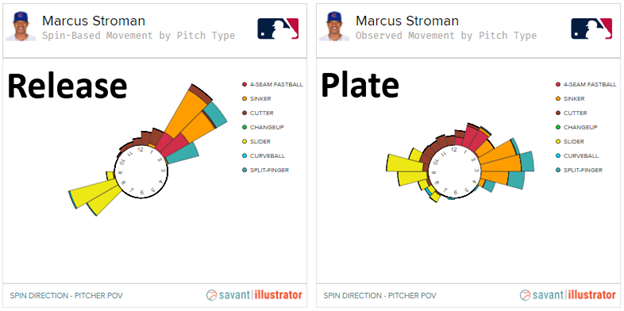
Here’s where it gets interesting. Compare the sinkers (and repertoires, really) of Spencer Turnbull and Marcus Stroman. First, the various spin directions of Stroman’s pitches, at release versus plate:

And then  Turnbull’s repertoire, at release versus plate:

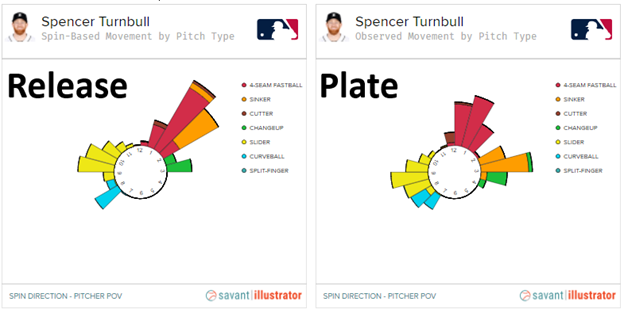
You’re looking at what many consider to be two of the most robust SSW profiles in MLB. By axis deviation, Stroman’s pitches all fan out, with his sinker and splitter shifting down and to his arm-side, and his slider shifting up and to his arm-side. That should make for pitches that not only repel one another but move more differently than they’re supposed to at release. The same is true for Turnbull, in that his sinker and changeup shift down and to his arm-side, with the lone difference being that his slider shifts down instead of up. Regardless, these should make for two repertoires with a lot more movement than expected at release. Right? Wrong!

Consider their repertoires by active spin, as well as expected and actual induced vertical break (IVB) and horizontal break (HB):

	Active Spin	xIVB	IVB	xHB	HB	Delta Sums
Turnbull, SI	78	6.5	7.1	14.5	17.2	3.4
Stroman, SI	59	4.4	4.1	11.3	10.2	1.4
Turnbull, CH	94	4.8	1.5	15.9	18.8	6.2
Stroman, FS	82	–	–	–	–	–
Turnbull, SL	35	1.1	-0.6	7.7	6.7	2.8
Stroman, SL	53	-1.1	1.3	12.1	11.0	3.6

If this table is overwhelming, then I might suggest honing in on the delta sums column, which takes the absolute value of the difference in IVB and expected IVB and adds it to the absolute value of the difference in horizontal break and expected horizontal break. What that number tells you is how many inches in total the given pitch moves differently than is expected based on the pitch’s characteristics at release.

You may be surprised to find that Stroman isn’t really an SSW darling at all. His sinker gets less arm-side movement than expected – in fairness, he also purportedly throws a one-seamer with SSW – and his slider gets less sink and sweep than expected too. Turnbull, on the other hand, is SSW’d up. He gets nearly three inches of added arm-side movement on both his sinker and changeup, but, like Stroman, his slider gets less sweep than expected at release despite an axis deviation that might suggest otherwise. All of this can be traced back to their significant differences in active spin. As mentioned before, SSW requires a certain gyro component to any given pitch but, as with most things, moderation is key.

Marcus Stroman‘s spin out of the hand vs. at the plate

Spencer Turnbull‘s spin out of the hand vs. at the plate

courtesy BaseballCloud’s BallR tool

Stroman has an intensely gyro-heavy sinker: he had the most inefficient sinker of all pitchers in 2021. Like our pure gyro slider example from before, his sinker moves through the air relatively unbothered, because there is less Magnus force applied to it than other sinkers. Because it’s so spin inefficient, though, it doesn’t give the seams sufficient opportunity to interact with the air and throw the pitch off its trajectory. And so, despite the robust axis deviation, his sinker isn’t an SSW pitch at all. Turnbull, on the other hand, has a significant gyro component to his sinker in particular, but he gets enough active spin (or transverse spin) for him to reap the benefits of Magnus movement, while orienting the ball in a way that he gets added non-Magnus movement too.

This is important information. If the spin tilt of Stroman’s pitches are changing in flight but not adding any movement to his pitches, then why should we care and, more importantly, why are we calling that SSW? My answer to both questions is the same: we shouldn’t.

This shows us that axis deviation shouldn’t be the sole focus in consideration of SSW. Ever. It can help explain a lot, but only when considered with the context of active spin and, perhaps even better, seam orientation. SSW can be achieved in different ways, all of which include getting the seams of the baseball to interact with the air. In the end, that has to do with the interaction of the gyro angle of the ball (i.e., its spin efficiency), as well as the orientation of the seams.

While axis deviation can tell us some information about SSW, sometimes it doesn’t tell us much of anything. There are pitchers who throw pitches with SSW with little axis deviation at all. Take a look at this slider from Spencer Patton:

Based on Patton’s pitch characteristics, his slider should get just under five inches of sweep, but as you can see, it gets a lot more than that. More specifically, it gets 12.5 inches of sweep, ranking him in the 99th percentile of non-Magnus sweep. It’s clear that this SSW isn’t coming via axis deviation, given that his slider ranks in the 38th percentile. That makes his slider a great example of a pitch that axis deviation doesn’t play much of a role in, in terms of SSW.

I’ll leave you with this. Consider the relationship between active spin and axis deviation on sinkers:

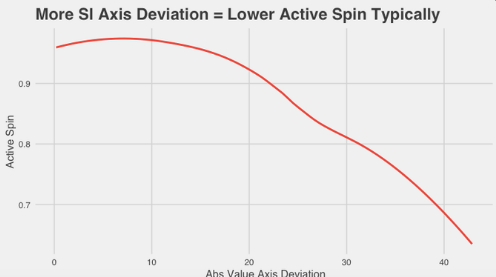
There’s a clear relationship between active spin and axis deviation. That is, the more gyro spin, the higher the axis deviation. That means that as you get into more gyro-heavy pitches, not only does the axis deviation start to lose meaning, but average spin direction becomes nearly meaningless.

I’ll show you what I mean with an extreme example. Consider Taylor Williams’ gyro slider:

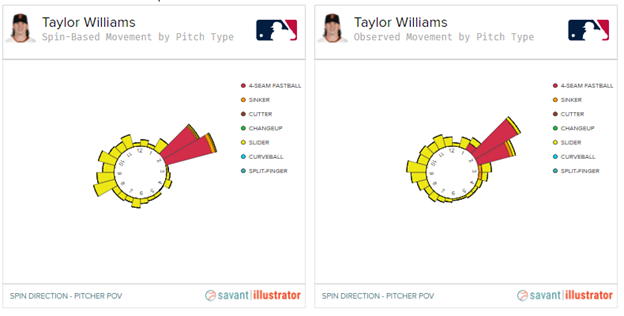
By axis deviation, Williams’ slider moves an entire hour on a clock face, from 9:00 to 10:00. All of these numbers, of course, are complete nonsense. Because Williams throws with almost pure gyro spin, his spin direction is reflected in all directions on a clock face, which means that it doesn’t make a whole lot of sense to take the average of the pitch’s spin direction. As the amount of gyro spin on a pitch increases, there reaches a point where axis deviation and spin direction begin to lose meaning. Not only because SSW effects aren’t taking place anymore, but because we’re taking the average of something that shouldn’t be averaged. It would be like considering the average velocity of Yu Darvish, who throws a 95 mph fastball and 75 mph curveball in an attempt to express how hard he throws on average. You wouldn’t.

Some proprietary models exist, like the one used above, in which we can compare actual movement versus expected movement. Any differences between the two can be chalked up to non-Magnus movement, although I say that with the caveat that the model mentioned above doesn’t include observed spin vector, making it good, usually, but flawed. Given that we don’t have public-facing information about seam orientation, we’ll have to pair metrics together, like spin efficiency and axis deviation, but it’s important to know that without seam orientation and observed spin vector, the puzzle is incomplete. Our understanding of SSW is evolving, and it’s certainly complicated. Still, if there’s anything to take away from here, it’s that axis deviation is far from the gold standard in terms of explaining SSW, and spin efficiency is a huge, underutilized factor to be considered.